Frequently Asked Questions about CO2 laser lenses for cutting

Frequently asked questions

Warranty information
Transportation and Payment Options
Technical info

What can I cut with a 100W or less CO2 laser?

How do I relate Intensity to laser power ?

What is all this TEMoo, M² and Gaussian beam all about?

I need to cut a very thin line. How small can I focus the laser beam?

What is 'depth of field?'

A useful table for lens focal length, Spot Size and DOF

Major cause of laser tube failure. Read this, please!

Fluorinert FC-77 AND fc-770 coolants for Sharplan medical lasers

Technical info.

The information in this page is a collection of odds and ends -- related to CO₂ lasers -- that you may find useful. We are not reporting anything new in this page as many others have written about and published them before. We will add more stuff to the page as time permits. After a few months (years!) we will try to index it or give it an outline. For now it is a juxtaposition of notes.

We apologize to the gurus of lasers for all the simplifications we have made.
If you are a laser guru, please skip this page.

A word about spot size (size of the focused beam)

Most applications of CO2 lasers, whether industrial cutting or medical surgery, require some degree of focusing the beam. The reason being that what actually does the cutting for you is not the raw power in the beam, i.e. 50 Watts, but it is the power density, i. e. how many Watts per unit area. Did I lose you ? Let's go back.

Let us say you have a 50 Watt laser. Let us also say that the 50 Watt beam of this laser, measured at about one (1) meter away from the laser head, has a beam diameter of 6 mm =1/4 inch. The area of a 6 mm circle is 28 sq mm. Hence your beam at that position has a power density (called intensity) of 50/28 =1.8 Watt per sq mm (or an intensity of 180 Watt/sq cm).

If there was something you could cut with this intensity, say some kind of thin plastic, then (a) the width of the cut would be 6 mm (one diameter) wide, which would not be a precision cut, and (b) you would have to go rather slow, which would then allow heat of the beam to propagate and set things on fire and that would not be good either!
It is like slicing bread with a very wide & dull knife.

Let us say you could turn a knob and increase the power of your laser to 500 Watts! Then we know that you spent upwards of $50,000 on this laser and both (a) and (b) above are still problems.

Maybe it would be easier, cheaper and wiser to reduce the area of the beam. That of course is done by using a lens in front of the beam. If you get a lens that can reduce the beam diameter from 6 mm to 0.6 mm ( i.e. 10 times smaller) the area would become 100 times smaller and therefore the power density (intensity) would be 100 times larger or 18,000 Watts per sq cm or 180 Watts per sq mm! Now we are up to something.

At 180 Watts per sq mm and 0.6 mm (0.02 inch) beam diameter, one can cut a lot of 'things' and cut them fast too. But you say, if I can easily focus the beam and reduce its diameter 10 times and increase its intensity 100 times, why don't I get a lens that reduces the diameter 100 times and therefore increase the intensity 10,000 times? Bright idea, but let us see why not.

There are fundamental laws of physics (bottle necks) that limit the size to which a beam of light (laser or otherwise) can be focused to. In our application, the first bottle neck says; even if all your tools (lasers & lenses) were perfect you can not focus a beam to a size smaller than its wavelength. The wavelength of CO2 laser is 10 micron (0.01 mm), therefore this is the smallest diameter of the circle it can be focused to.

We will explain these bottle necks in a little more detail later on but if you prefer not to read anymore, here it is:
If we remove the perfect assumption (the lens is not perfect and the laser is not perfect) then you would be doing amazingly good if your lens and laser are good enough to give you a spot size of 100 micron diameter ( 0.1 mm ). You will be doing excellent if you get 200 micron ( 0.2 mm ) and very good if you get 300 micron ( 0.3 mm ).

In real life you have to compromise. The cost of a lens that gives you 0.1 mm spot diameter could be 10 times the cost of the one that gives you 0.3 mm spot diameter.

More important, from the practicality point of view, you need to have some 'working distance' from the output of the lens to the surface you are working on. If, to get a small spot, you choose this distance to be very short (say 1/2 inch = 12 mm) then all the junk you are cutting will splash back into your lens and destroy it in no time (and these lenses are not cheap!). Furthermore, a very short focal length lens does not have any 'depth of focus'. That means your 'cone' of light opens up too quickly and you can not cut anything that has much thickness.

Again we come back to the compromise issue. Once you choose a working distance of say 100 mm = 4 inches, then you have automatically chosen to live with a bigger spot than you would have at 1/2 inch.

Conclusions:

a) Spot size can not arbitrarily be made 'small'. The smallest theoretical diameter is, roughly, wavelength of the beam.

b) The smallest theoretical diameter can not be achieved practically and we would be extremely happy if we can come to a factor of 10 of that limit.

c) Real life situations demand long 'working distances' and long depth of focus. That means another factor of 5 or so lager spot size diameter.

Therefore, if you get a CO₂ laser and an ordinary (affordable) ZnSe lens, you should be happy to get a spot size diameter anywhere from 250 to 500 micron = 0.25 to 0.5 mm diameter. From your spot diameter you can calculate the spot area and from there you can calculate your beam intensity at any power setting.

Intensity = Power / spot size area

The intensity of the aforementioned 50 Watt laser at 0.4 mm spot size ( 400 micron ) would be 400 W/sq mm or 40,000 W/sq cm. If you don't need that much intensity, lower the laser power (to let us say 12 Watts) and the intensity will be less (100 W/sq mm at 12W). Or you can run the laser at a lower duty cycle, say 50% duty cycle, by pulsing it. For example, 50 ms pulses 10 times a second will half the power.

Here are some numbers for a 50 Watt laser, 6 mm beam & M ²=1.1:

working distance, mm spot diameter, mm Intensity at focal point, W/sq mm

400
100
25
1
.25
.06*
65
1000
16,000

* this is difficult to achieve

Some typical 'stuff' you can cut with a medium power ( < 100W ) laser and the speed of cut is shown below. For a more extensive application file, please check CO2 Laser Applications in Cutting.

Process Power density, W/sq mm Process rate

Cutting thin plastic
( 3 to 5 mil =
.07 to .13 mm) 30 - 70
15 to 30 in/min
380 to 760 mm/min

Decorative engraving of hard wood 70 - 110
4 in/min for 1/8 to 1/16 deep
100 mm/min for 1.5 to 3 mm deep

Hole punching, soft wood 40 - 100
0.075 inch per 0.1 second

Tissue removal 10 - 100

Cautery 5 - 10

Remember we calculated the power density (intensity) of a 50 Watt laser at 0.4 mm spot size ( 400 micron ) was 400 W/sq mm. Therefore you can see that, unless you are into serious cutting of metals, you don't really need anything more than a 100 Watt laser and good focusing optics.

Back to where you were!

Some more detail on the 'bottle necks'.

1. The laser beam contribution. Theoretical laser beams have this property (you must have heard of) called TEMoo. Let us again assume you have obtained a perfect laser with a perfect TEMoo beam. The smallest size you can focus this beam to (assume the lens is perfect too ) is:

proportional to the wavelength
proportional to the focal length of the lens
inversely proportional to the diameter of the beam.

Therefore to minimize spot size due to laser beam properties (diffraction and divergence) we want the largest beam diameter and the shortest focal length

2. The lens contribution. Suppose you ask an optics manufacturer to design and then manufacture the best possible lens that man can make for your particular application (we are already losing the game because this by itself is not realistic; no one could afford such a lens for industrial applications). Even if you did, lenses have this particular properties called 'aberrations' and one of them, the spherical aberration is the next bottle neck that will limit the size of our focused beam.

What is it, you ask? In short, the rays of light that impinge on the lens further away from the lens center, come to focus (at the other side) nearer to the lens. It has the effect of increasing the size of the focused beam in addition to causing 'best focus' occur at a different location than the calculated focal point.

Therefore if our laser beam is 6 mm wide and we use a 6 mm diameter, 6 mm focal length ZeSe meniscus lens (not very common!), the beam could measure 0.1 mm = 100 micron in diameter. (Note that, in the example, we chose ZnSe as our lens material and meniscus as its shape, good for CO₂. Spherical aberration is material/wavelength dependent; visible light requires a plano-convex shape for minimum spherical aberration).

What this means to us is this; as long as a laser beam has a diameter, there will be a spread of 'focal point' and the 'focal point' is not really a 'point'.

This kind of aberration increases rapidly as diameter of the beam increases (goes as D³ )and decreases rapidly as the focal length of the lens increases (goes as 1/f ²). Can you see how nature is fighting us? To reduce spherical aberration (a property of lenses), we want the smallest beam diameter and the longest focal length lens.

Remember 3 paragraphs ago? To minimize spot size that comes about from laser properties (diffraction, divergence) we wanted the largest beam diameter and the shortest focal length.

As you see, these two will always fight each other and compromises have to be made. In addition no man made, affordable lens is perfect and no real laser beam can be a truly perfect TEMoo (diffraction limited beam), that is a reality of life. They maybe called close to perfect but never perfect.!

Further down we continue the TEMoo discussion but for now let us reiterate our conclusions:
a) Spot size can not arbitrarily be made 'small'. The smallest theoretical diameter is, roughly, wavelength of the beam.
b) The smallest theoretical diameter can not be achieved practically and we would be extremely happy if we can come to a factor of 10 of that limit.
c) Real life situations demand long 'working distances' and long depth of focus. That adds another factor of 5 or more to the spot size diameter.

TEMoo. For a long time, laser manufacturers were trying to come up with a universal parameter that could characterize the 'perfectness' of their laser beam (how close it is to TEMoo ) and they could tell each other 'my beam is better than yours'! A convenient parameter was defined and is now called M² (M squared). By definition it is larger than one (1) (M²=1 means perfect) and how it is measured, depends on whom you ask. If you don't know where to put it in an equation, the rule is: where it will do the most damage! The size of the beam is M² times larger, the divergence is M² times worse and so on. M² measures how close the actual laser beam is to a theoretical TEMoo beam profile (keep on reading!).

TEMoo is a property of the beam that is determined by the physical construction of your laser. The designer has to choose some mirrors for the laser, has to choose some length for the laser and has to choose a cross section for his laser beam (these chosen boundaries cause diffraction which is bad). There always has to be a compromise between the above three and output power and then between output power and final price of the product.

If you want to design a Ferrari, it can't be as spacious as a van.

A theoretical TEMoo beam has a perfect Gaussian profile. A Gaussian profile means the cross section of the beam is 'bell shaped' (higher intensity at the center and falling off as you go away from the center).

Now there are 'bell shapes' and there are 'bell shapes'. Most 'distribution curves' (sorry) are 'bell shaped' but not all are Gaussian. There is one parameter that completely determines a 'bell'. It is the 'Full Width at Half Max, FWHM' (or FWHH 'H'= Height). No "bell shaped' distribution curve can go from maximum-to-zero faster than a Gaussian of the same FWHM. That is what sets the Gaussian apart from the rest of the 'bells'.

For our discussion of the laser beam, the chosen parameters of the laser structure determine the FWHM of the expected perfect TEMoo beam. The real output beam, however, will be 'nearly Gaussian' ( a term used before the invention of M²). It will be 'bell shaped', it will be reproducible and most importantly it will be predictable (all aspects of its focussibilty and projection can be calculated) but it will never fit a Gaussian of the same FWHM.

Why say all this? Remember that we said a perfect beam (sometimes called diffraction limited) would focus to the smallest spot size. If it is not perfect, its M² is larger than one (1), then it has excess divergence and will focus to a larger size than a perfect beam would.

A laser beam - due to diffraction and beam divergence which in turn are related to dimensions being finite - will focus to a spot size that is directly proportional to the focal length of the lens and inversely proportional to the diameter of the laser beam at the point it meets the lens. The formula is:

spot dia. = 1.27 x f x wavelength x M² / D
where D is the beam diameter at lens position (generally smaller than the lens diameter).

In our particular case of CO₂ laser, the wavelength is 10.6 micron, so the above relation becomes;

spot dia. (in mm) = 0.013 x M² x f / D

p.s. Use the same unit (cm or inches) for ' f ' and 'D' and the size of the spot will be in mm

So everything is fighting us even if M² was 1!! You need large D to focus the beam to smaller spot but large diameter laser beams can not be made to be TEMoo and large diameter lenses are expensive like crazy). At the same time you need a short focal length lens to make the spot small but very short focal length lenses are difficult, expensive an impractical to manufacture.

What a mess! It's a miracle it all works!!

Depth of Field

The above formula lets us calculate the spot size, or the diameter of the laser beam, at the focal point of a given lens. Let us visualize that the beam goes through the lens and converges like a ' cone ' to a point and then diverges as we go away from the apex of the cone. Let us think of two cones with their apex attached. The question before us is this;

If at the focal point of the lens (the apex of the two cones) the beam is of a given size, how far away from this point is the beam still in good focus (i.e. of usable size)? Is 0.01 mm away still good focus? How about 1 mm away? 10 mm?

The answer to this question defines the Depth Of Field (DOF). It has been decided, more or less arbitrarily, that 'DOF is the range along which the size of the beam is no more than 1.4 times the minimum spot size'

Let us explain. Suppose the focal point is at position zero and the spot size at this point is 200 micron = .2 mm =0.008" (this is the apex of the two cones). How far do we have to go before the spot size increases to 280 micron? What is so special about 280 micron? Nothing. It is just that, by convention, you keep on moving away from the minimum spot size until the spot size is 40% larger. You stop and measure how far from the minimum spot size you have moved. This is half the Depth of field (the other half is on the other side of the focal point!. Did I lose you? Call the distance you moved away ' d ' . Twice this distance ( one 'd' in front and one 'd' before the exact focal point = a distance of '2d' ) is defined as the Depth Of Field. Notice that all along this range the spot size is no more than 1.4 times the minimum spot size.

You can usually place your object -- to be cut or to be marked or to be vaporized -- anywhere within this range, in front of the lens.

You may think this is a large distance but it usually is not. First let us write down the formula for calculating this range and then try some numbers.

DOF = 2.5 x wavelength x ( f /D )²

where D is the beam diameter and f is the focal length of the lens.

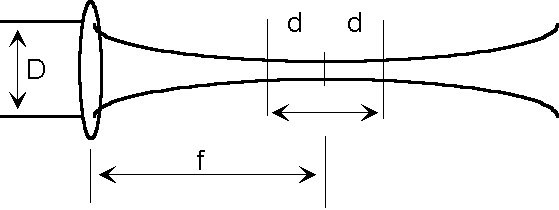
For CO₂ laser (wavelength = 10 micron = 0.01 mm), this becomes:

DOF (in mm) =0.027 x ( f / D )²

Example 1:

With a f = 100 mm (4 inch) focal length lens and a beam diameter of 6 mm we get (assume M²=1)
spot size = .013 x 100/6 = 0.2 mm = 200 micron
and
DOF = 0.027 x (100/6)² = 7.5 mm

Example 2:

See what happens if you use a f = 50 mm (2 inch) lens to get four times the intensity and half the spot size;
spot size = 0.013 x 50/6 = .1 mm = 100 micron
small spot size and high intensity, BUT
DOF = .027 x (50/6)² ~ 2 mm. Not much!

Example 3:

What happens if we go the other way; f = 20 cm = 8 inches. Then,

spot size is twice the original size and DOF is 4 times bigger
spot size = .013 x 200/6 = 0.4 mm = 400 micron
and
DOF = 0.027 x (200/6)² = 30 mm

So if you can live with a larger spot size, then the positioning of your final piece becomes much less critical.

Suppose you insist on having it both ways. "I want longer working distance and a small spot".

No problem. One other parameter that we have not touched is the beam diameter. Remember the formulae,

spot dia. (in mm) = 0.013 x M² x f / D

and

DOF (in mm) =0.027 x ( f / D )²

Suppose we use a Beam Expander (usually 2 lenses) to increase the diameter of the beam, say, 3 times. Then, D=18 mm or about 3/4".

Then in example 3 above the numbers will become,

Example 4:

D=18 mm, f=8" (working distance of 8 inches), then
spot size = 130 micron (not too bad)
and
DOF = 3.3 mm (respectable).

So as you can see, you can play this game until it meets your particular needs and requirements.

Spot Size & Depth Of Field for some standard lenses calculated for beam diameter at lens position = 7 mm and M^2 =1
Lens Focal Length, mm (inch)	Spot Size		Depth Of Field
Lens Focal Length, mm (inch)	u m	inch	mm	inch
12.7 (1/2)	23	0.001	86 um	0.003
19 (3/4)	37	0.001	0.2 mm	0.008
25.4 (1)	49	0.002	0.35	0.014
38 (1.5)	73	0.003	0.80	0.03
51 (2)	98	0.004	1.4	0.05
76 (3)	147	0.006	3.1	0.12
101 (4)	195	0.008	5.6	0.2
127 (5)	245	0.010	8.8	0.34
152 (6)	290	0.011	12.6	0.5
Notes: -- Values are calculated from the formula for spot size = 0.013 x f / D where D is beam diameter at lens position. -- 'D' may be increased 2 or 3 times by using a 'beam expander' -- which means spot size will be decreased by the same factor -- and DOF will be decreased by the square of that factor. To be continued !

Table of Contents

Web page created and maintained by Parallax Marketing Department.

Parallax Technology, Inc.